Geometría analítica.
Se conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometria diferencial con Gauss y más tarde con el desarrollo de la geometría algebraica.
Los dos problemas fundamentales de la geometría analítica son:
- Dado el lugar geométirco en un sistema de coordenadas, obtener su ecuacion.
- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que la cumplen.
Lo novedoso de la Geometría Analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función u otro tipo de expresión matemática. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ).
Construcciones fundamentales.
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados "abscisa" y "ordenada" del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la Geometría Analítica.
Con la Geometría Analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Éste es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Localización de un punto en el plano cartesiano
En un plano traza dos rectas perpendiculares (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordendas, quedará representado por un par ordenado (x,y), siendo x la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e y la distancia al otro eje (al horizontal).
En la coordenada x, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada y, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso). A la coordenada x se la suele denominar abscisa del punto, mientras que a la y se la denomina ordenada del punto.
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a 0, así que serán de la forma (x,0), mientras que los del eje de ordenadas tendrán abscisa igual a 0, por lo que serán de la forma (0,y).
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia 0 a cada uno de los ejes, luego su abscisa será 0 y su ordenada también será 0. A este punto —el (0,0)— se le denomina origen de coordenadas.
Ecuaciones de la recta en el plano
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
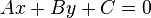
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la función polinomica de primer gardo de la forma:
como expresión general, Esta es conocida como ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
-
Rectas oblicuas. Rectas horizontales. Rectas verticales.
- Rectas verticales, estas rectas no cortan al eje de ordenadas y son paralelas a dicho eje y se denominan rectas verticales. El punto de corte con el eje de abscisas es el punto (x0,0). La ecuación de dichas rectas es:
- Rectas horizontales, estar rectas no cortan al eje de las abscisas y, por tanto, son paralelas a dicho eje y se denominan rectas horizontales. El punto de corte con el eje de ordenadas es el punto (0,y0). La ecuación de dichas rectas es:
- Rectas oblicuas. Cualquier otro tipo de recta recibe el nombre de recta oblicua. En ellas hay un punto de corte con el eje de abscisas (a,0) y otro punto de corte con el eje de ordenadas (0,b). El valor a recibe el nombre de abscisa en el origen, mientras que el b se denomina ordenada en el origen.
Secciones cónicas
El resultado de la intersección de la superficie de un cono, con un plano, da lugar a lo que se denominan secciones cónicas, que son: la parábola, la elipse (la circunferencia es un caso particular de elipse) y la hipérbola.
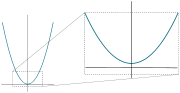
- La parábola es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
Una parábola (Figura A) cuyo eje de simetría sea paralelo al eje de abcisas se expresa mediante la ecuación:
- Elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
Una elipse (Figura B) centrada en los ejes, con longitudes de semieje a y b viene dada por la expresión:
- Si los dos ejes son iguales y los llamamos c:
- el resultado es una circunferencia:
- La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia (resta) de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
La hipérbola (Figura C) tiene por expresión:
Construcciones en el espacio tridimensional
Los razonamientos sobre la construcción de los ejes coordenados son igualmente válidos para un punto en el espacio y una terna ordenada de números, sin más que introducir una tercera recta perpendicular a los ejes X e Y: el eje Z.
Sin embargo no hay análogo al importantísimo concepto de pendiente de una recta. Una única ecuación lineal del tipo:
ax + by + cz = 0
Representa en el espacio un plano. Si se pretende representar mediante ecuaciones una recta en el espacio tridimensional necesitaremos especificar, no una, sino dos ecuaciones lineales como las anteriores. De hecho toda recta se puede escribir como interesección de dos planos. Así una recta en el espacio podría quedar representada como:
Es importante notar que la representación anterior no es única, ya que una misma recta puede expresarse como la intersección de diferentes pares de planos. Por ejemplo los dos pares de ecuaciones:
Clasificación de la geometría analítica dentro de la geometría
Desde el punto de vista de la clasificación de Klein de las geometrías (el programa de Erlagen), la geometría analítica no es una geometría propiamente dicha.
Desde el punto de vista didáctico, la geometría analítica resulta un puente indispensable entre la geométria euclidiana y otras ramas de la matemática y de la propia geométria, como son el propio análisis matemático, el álgebra lineal, la geométria afin, la geométria diferencial o la geométria algebraica.
Historia de la geometría analítica
Existe una cierta controversia sobre la verdadera paternidad de este método. Lo único cierto es que se publica por primera vez como "Geometría analítica", apéndice al Discurso del método, de Descartes, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Aunque Omar Khayyam ya en el siglo XI utilizara un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuvieran acceso a su obra.
El nombre de geometría analítica corrió parejo al de geometría cartesiana, y ambos son indistinguibles. Hoy en día, paradójicamente, se prefiere denominar geometría cartesiana al apéndice del Discurso del método, mientras que se entiende que geometría analítica comprende no sólo a la geometría cartesiana (en el sentido que acabamos de citar, es decir, al texto apéndice del Discurso del método), sino también todo el desarrollo posterior de la geometría que se base en la construcción de ejes coordenados y la descripción de las figuras mediante funciones —algebraicas o no— hasta la aparición de la geometría diferencial de Gauss (decimos "paradójicamente" porque se usa precisamente el término "geometría cartesiana" para aquello que el propio Descartes bautizó como "geometría analítica"). El problema es que durante ese periodo no existe una diferencia clara entre geometría analítica y análisis matemático —esta falta de diferencia se debe precisamente a la identificación hecha en la época entre los conceptos de función y curva—, por lo que resulta a veces muy difícil intentar determinar si el estudio que se está realizando corresponde a una u otra rama.
La geometría diferencial de curvas sí que permite un estudio mediante un sistema de coordenadas, ya sea en el plano o en el espacio tridimensional. Pero en el estudio de las superficies, en general, aparecen serios obstáculos. Gauss salva dichos obstáculos creando la geometría diferencial, y marcando con ello el fin de la geometría analítica como disciplina. Es con el desarrollo de la geometría algebraica cuando se puede certificar totalmente la superación de la geometría analítica.
Es de puntualizar que la denominación de analítica dada a esta forma de estudiar la geometría provocó que la anterior manera de estudiarla (es decir, la manera axiomático-deductiva, sin la intervención de coordenadas) se terminara denominando, por oposición, geometría sintética, debido a la dualidad análisis-síntesis.
Actualmente el término geometría analítica sólo es usado en enseñanzas medias o en carreras técnicas en las que no se realiza un estudio profundo de la geometría.
Parábola (matemática)
En matemática, la parábola (del griego παραβολή) es una sección cónica generada al cortar un cono recto con un plano paralelo a la directriz.[1]
Se define también como el lugar geométrico de los puntos que equidistan de una recta (eje o directriz) y un punto fijo llamado foco.
La parábola aparece en muchas ramas de las ciencias aplicadas, debido a que las gráficas de ecuaciones cuadráticas son parábolas. Por ejemplo, la trayectoria ideal del movimiento de los cuerpos bajo la influencia de la gravedad.
Historia
La tradición reza que las secciones cónicas fueron descubiertas por Menecmo en su estudio del problema de la duplicación del cubo,[2] donde demuestra la existencia de una solución mediante el corte de una parábola con una hipérbola, lo cual es confirmado posteriormente por Proclo y Eratóstenes.[3]
Sin embargo, el primero en usar el término parábola fue Apolonio de Perge en su tratado Cónicas,[4] considerada obra cumbre sobre el tema de las matemáticas griegas, y donde se desarrolla el estudio de las tangentes a secciones cónicas.
Es Apolonio quien menciona que un espejo parabólico refleja de forma paralela los rayos emitidos desde su foco, propiedad usada hoy en día en las antenas satelitales. La parábola también fue estudiada por Arquímedes, nuevamente en la búsqueda de una solución para un problema famoso: la cuadratura del círculo, dando como resultado el libro Sobre la cuadratura de la parábola.
Propiedades geométricas
Aunque la definición original de la parábola es la relativa a la sección de un cono recto por un plano paralelo a su directriz, actualmente es más común definir la parábola como un lugar geométrico:
|
De esta forma, una vez fija una recta y un punto se puede construir una parábola que los tenga por foco y directriz de acuerdo a la siguiente construcción. Sea T un punto cualquiera de la recta directriz. Se une con el foco dado F y a continuación se traza la mediatriz (o perpendicular por el punto medio) del segmento TF. La intersección de la mediatriz con la perpendicular por T a la directriz da como resultado un punto P que pertenece a la parábola. Repitiendo el proceso para diferentes puntos T se puede aproximar tantos puntos de la parábola como sea necesario.
De la construcción anterior se puede probar que la parábola es simétrica respecto a la línea perpendicular a la directriz y que pasa por el foco. Al punto de intersección de la parábola con tal línea (conocida como eje de la parábola) se le conoce como vértice de la parábola y es el punto cuya distancia a la directriz es mínima. La distancia entre el vértice y el foco se conoce como Distancia focal o Radio focal.
Lado recto
Al segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz, se le conoce como lado recto.
|
Siendo D, E los extremos del lado recto y T, U las respectivas proyecciones sobre la directriz, denotando por W la proyección del foco F sobre la directriz, se observa que FEUW y DFWT son cuadrados, y sus lados miden FW=2FV. Por tanto el segmento DE es igual a 4 veces el segmento FV (la distancia focal).
Las tangentes a la parábola que pasan por los extremos del lado recto forman ángulos de 45° con el mismo, consecuencia de que FEUW y DFWT sean cuadrados, junto con la construcción mencionada en la sección anterior. Además, tales tangentes se cortan en la directriz, precisamente en el punto de proyección W del foco, propiedades que pueden ser aprovechadas para construir una aproximación geométrica del foco y la directriz cuando éstos son desconocidos.
Semejanza de todas las parábolas
Dado que la parábola es una sección cónica, también puede describirse como la única sección cónica que tiene excentricidad e = 1. La unicidad se refiere a que todas las parábolas son semejantes, es decir, tienen la misma forma, salvo su escala.
Desafortunadamente, al estudiar analíticamente las parábolas (basándose en ecuaciones), se suele afirmar erróneamente que los parámetros de la ecuación cambian la forma de la parábola, haciéndola más ancha o estrecha. La verdad es que todas las parábolas tienen la misma forma, pero la escala (zoom) crea la ilusión de que hay parábolas de formas diferentes.
Un argumento geométrico informal es que al ser la directriz una recta infinita, al tomar cualquier punto y efectuar la construcción descrita arriba, se obtiene siempre la misma curva, salvo su escala, que depende de la distancia del punto a la directriz.
Tangentes a la parábola
Un resultado importante en relación a las tangentes de una parábola establece:
|
En lo sucesivo, F denotará el foco de una parábola, P un punto de la misma y T su proyección sobre la directriz. Retomando la construcción dada para encontrar puntos de una parábola, sea MP la mediatriz del triángulo FPT, el cual es isósceles y por tanto biseca al ángulo FPT. Lo único que hay que verificar ahora es que MP también es la tangente en el punto P. Sea Q otro punto de la parábola y sea U su proyección en la directriz.
Puesto que FQ=QU y QU
Aplicaciones prácticas
Una consecuencia de gran importancia es que la tangente refleja los rayos paralelos al eje de la parábola en dirección al foco. Las aplicaciones prácticas son muchas: las antenas satelitales y radiotelescopios aprovechan el principio concentrando señales recibidas desde un emisor lejano en un receptor colocado en la posición del foco.
La concentración de la radiación solar en un punto, mediante un reflector parabólico tiene su aplicación en pequeñas cocinas solares y grandes centrales captadoras de energía solar.
Análogamente, una fuente emisora situada en el foco, enviará un haz de rayos paralelos al eje: diversas lámparas y faros tienen espejos con superficies parabólicas reflectantes para poder enviar haces de luz paralelos emanados de una fuente en posición focal. Los rayos convergen o divergen si el emisor se deplaza de la posición focal.
| Los radiotelescopios concentran los haces de señales en un receptor situado en el foco. El mismo principio se aplica en una antena de radar. | Cocina solar de concentrador parabólico. El mismo método se emplea en las grandes centrales captadoras de energía solar. |
Ecuaciones de la parábola
Con el advenimiento de la geometría analítica se inició un estudio de las formas geométricas basado en ecuaciones y coordenadas.
Una parábola cuyo vértice está en el origen y su eje coincide con el eje de las ordenadas, tiene una ecuación de la forma y=ax2 donde el parámetro a especifica la escala de la parábola, incorrectamente descrita como la forma de la parábola, ya que como se dijo antes, todas las parábolas tienen la misma forma. Cuando el parámetro es positivo, la parábola se abre «hacia arriba» y cuando es negativo se abre «hacia abajo».
Si bien, la expresión en forma de ecuación no fue posible hasta el desarrollo de la geometría analítica, la relación geométrica expresada en la ecuación anterior ya estaba presente en los trabajos de Apolonio,[2] y se bosquejará a continuación usando notación moderna.
Tomando nuevamente la definición de parábola como sección de un cono recto de forma paralela a la directriz, sea V un punto en el eje y sea QV perpendicular al eje. (QV corresponde al valor xPV al valor y). Considerando la sección circular que pasa por Q y es paralela a la base del cono, obtenemos H, K paralelos a B y C. en la versión analítica y
Por el teorema de potencia de un punto:
.
Al ser PM paralela a AC, los triángulos HVP, HKA y BCA son semejantes y así:
.
Usando nuevamente los paralelismos:
.
Despejando HV y VK para sustituir en la fórmula de QV² resulta en
.
Pero el valor de  es una constante pues no depende de la posición de V, por lo que haciendo
es una constante pues no depende de la posición de V, por lo que haciendo
arroja la expresión moderna y=ax².
Aplicando una sustitución de coordenadas podemos obtener ahora la ecuación de una parábola vertical para cualquier posición de su vértice.
|
agrupando los términos y reordenando se obtiene una forma equivalente:
|
Si la parábola es horizontal, se obtienen ecuaciones similares pero intercambiando y por x y viceversa. Así tendríamos:
|
Ecuación involucrando la distancia focal
Pueden haber muchas parábolas que tengan un mismo vértice (variando el parámetro a) en la primera ecuación. Sin embargo, dados dos puntos fijos, existe sólo una parábola que los tiene por vértice y foco ya que la directriz queda automáticamente fija como la perpendicular a la línea que une el foco con el vértice y a esa misma distancia del último.
Consideremos el caso especial en que el vértice es (0,0) y el foco es (0,p). La directriz es por tanto, la recta horizontal que pasa por (0,-p). A la distancia entre el vértice y el foco se le llama distancia focal, de modo que en este caso la distancia focal es igual a p. Con esta configuración se tiene:
|
De forma alterna:
|
Es de notar que el coeficiente 4p es precisamente la longitud del lado recto de la parábola.
Ambas ecuaciones se refieren a parábolas verticales que se abren «hacia arriba». La ecuación de una parábola que se abre hacia abajo es similar excepto que varía un signo. En este caso, el foco sería (0,-p) y de esta forma:
|
Cuando la parábola es horizontal «hacia la derecha», se obtiene una ecuación similar intercambiando los roles de x, y:
|
obteniendo mediante un cambio de signo la ecuación de las parábolas hacia la izquierda.
Finalmente, las ecuaciones cuando el vértice no está en el centro se obtienen mediante una traslación. En el caso común de la parábola vertical hacia arriba se tiene
|
mientras que para la parábola horizontal se intercambia x con y:.
|
Ecuación general de una parábola
Hasta ahora se han descrito parábolas con sus ejes paralelos a alguno de los ejes de coordenadas. De esta forma las fórmulas son funciones de x ó de y. Pero una parábola puede tener su eje inclinado con respecto a un par de ejes de coordenadas ortogonales.
|
Mediante traslaciones y rotaciones es posible hallar un sistema de referencia en el que la ecuación anterior se exprese mediante una fórmula algebraica de la forma
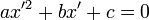 , donde a es distinto de cero.
, donde a es distinto de cero.








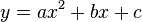

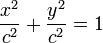

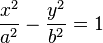
















 .
.
 .
. .
. .
. ,
, ,
,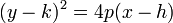 .
.
No hay comentarios:
Publicar un comentario